Impact of more than one Constraint -3

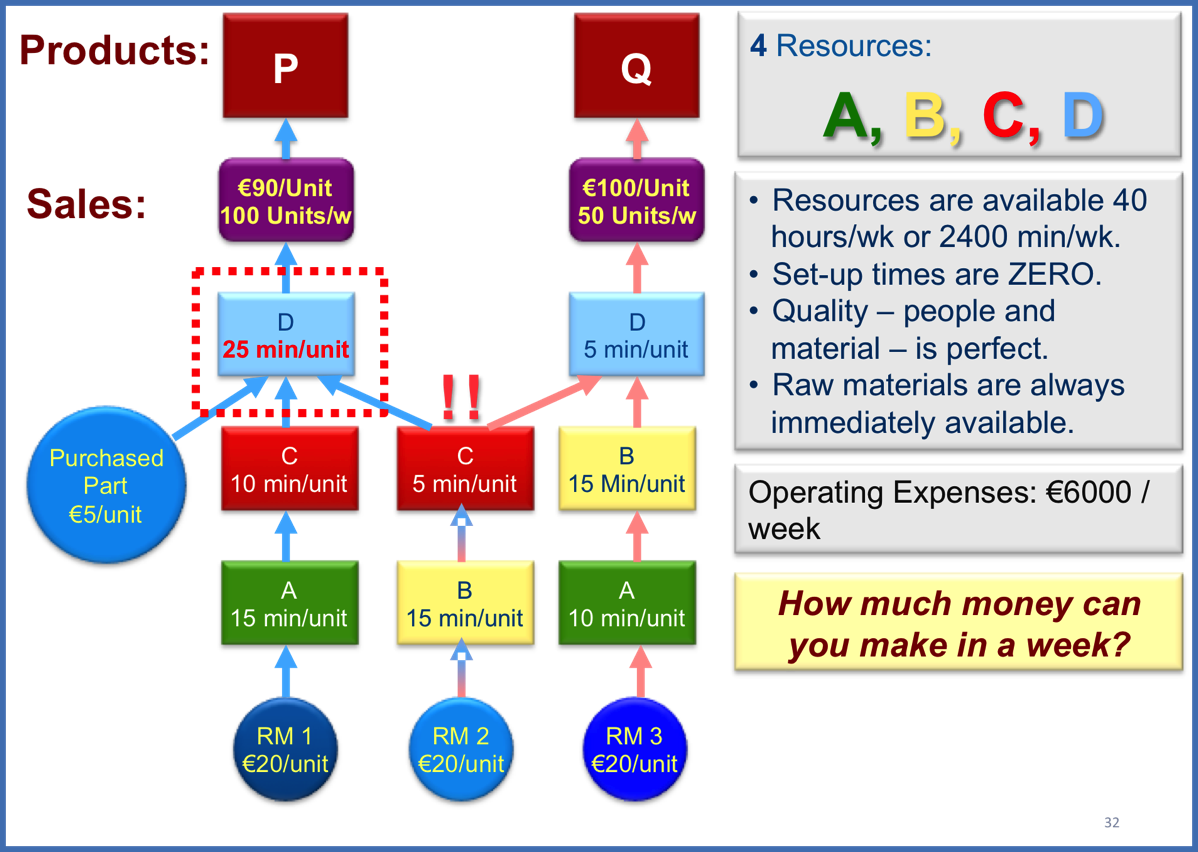
The P - Q thought experiment with 2 constraints

 

Alan Barnard (at the 2006 TOC-ICO conference) asked the question whether the simple Throughput per Constraint Unit rule is valid with 2 (or more) overloaded resources. Alan used Eli Goldratt’s P-Q thought experiment for his discussion. His question is important because it is common to see businesses reduce ‘excess’ capacities to balance (or almost balance) capacities. The practice often results in two) or more concurrent constraints or ‘almost’ constraints. Since 2006 I have observed several factories that wonder why their output collapses below the theoretical capacity of their (almost) balanced lines.

I plan to show that that the Throughput per Constraint Unit rule continues to be valid using the same P-Q thought experiment. I also want to discuss this result in relation to the real World – how should companies manage resource capacities.

I would like readers to follow Eli Goldratt’s recommendation that they solve the problems – before I provide the solution and before my discussion of results. The learning experience will be greater and readers should be better able to discuss and critique my conclusions. If you are familiar with the thought experiment you can jump to the second part of this article. 

The key part of the article comes at the end when the solution used in the P-Q thought experiment is discussed in relation to REALITY. The thought experiment should not lead managers to an easy solution. The tool is useful but requires thought and care.

Most of us ‘solve’ the problem without much thinking. It’s like a simple arithmetic problem from grade school. From groups we usually get quite number of ‘wrong’ answers – some from arithmetic mistakes, some from faulty thinking. Below you will find the answers from inadequate thinking and the explanation for the ‘right’ solution.

The only change in my little factory is the amount of time needed at D to produce 1 P. The time has increased from 15 to 25 minutes. Check it for yourself - both Band D machines have insufficient capacity to produce all the weekly demand.

 

Below is the table showing how many minutes of each resource would be required to produce all the P and Q demand.

 

Our simple rule to use Throughput per constraint unit is in difficulty – we have 2 constraints. But B is still the most constraining unit so lets try the rule. The table below shows the result.

The rule does not seem to work. But we do have the more important rule that tells us to decide how to exploit the constraint (here we choose B, the more constraining resource). But to consume all the valuable B minutes we must have at least some D capacity available. So, we plan to sacrifice some P sales to liberate D capacity and make Q sales possible and to consume the primary (B) constraint’s capacity. B has 960 minutes of capacity available - enough to produce 32 Qs. To produce 32 Qs, I need 160 minutes; I must sacrifice 7 Ps.  BUT Sacrificing 7 Ps gives me 15 additional B minutes. I cannot use these to produce at the B machine (I need at least 30 minutes at B for 1 more Q).

Let’s sacrifice 8Ps and produce 36 Qs to consume all of B’s capacity – will our profits improve? Our secondary constraint (D) will still have 20 minutes of unused capacity after producing the 36 Qs.

 

This looks good; but we still have 20 minutes of D capacity left with which we could produce up to 4 Qs. Lets produce just 1 more Q, which requires us to give up 2 Ps, but might increase profit.

Not quite as good. 1 additional Q delivers 60€ more Throughput while giving up 2 of P costs 90€ Throughput – net we lose 30€ with every additional Q we produce. Not a good way to go. So lets try the other way – produce 1 more P.

Also, not so good since we gain 45€ from 1 extra P but lose 60 from 1 less Q (net we lose 15€); AND we have 15 minutes of unexploited B left over. These 15 minutes would be enough for 1 added P. But by producing 1 P, we need 25 minutes of D capacity, which we no longer have. It looks like we have found the maximum profit possible, 120€/week.

By introducing a second constraint into the P-Q experiment the maximum possible is cut by more than 50%.

The rules to followed were

1. Find the constraint (the most constraining resource).
2. Decide how this resource is to be exploited.
3. Subordinate everything else to that decision.

If we follow these 3 rules we should always find our way to the best mix to maximises our profit. (Alan Barnard used linear programming to find the same result.

In the next post I will discuss the impact of interactive constraints - like B and D are.

 

 

Fall in the Canadian sub-arctic - near Baie Comeau Oct. 1955